Système de coordonnées Polaires
Définition
\(\triangleright\) Définition d'une base polaire :
La base polaire est une base rotative orthonormé liée au système étudié et est définie par les vecteurs (\(\vec {e_r}, \vec{e_\theta}\)).
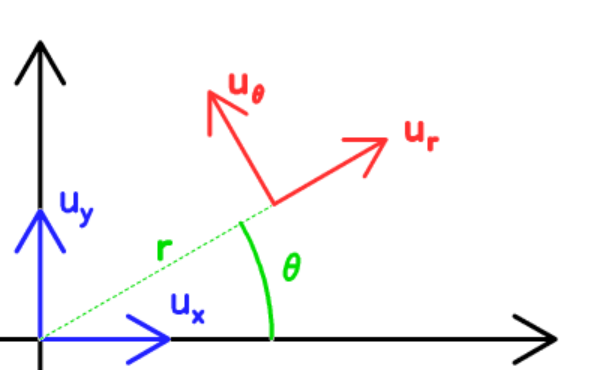Le vecteurs \(\vec e_r\) est définie dans le prolongement du rayon \(r\) lié à un référentiel fixe fixe
Le vecteurs \(\vec e_\theta\) est définie parralèlement au vecteur \(\vec e_r\).
Remarques
\(\triangleright\) Remarque sur la base polaire :
La base (\(\vec {e_r}, \vec{e_\theta}\)) est une base tournante basé sur \(\theta\)
Relations de passages
\(\triangleright\) Relations de passages de la base polaire :
$$(x,y) \iff (r,\theta)$$
$$(\vec i, \vec j)\iff(\vec{e_r},\vec{e_\theta})$$
- \(\begin{cases}x={{\vec{OM}.\vec i.cos\theta}} = {{r.cos\theta}}\\ y={{\vec{OM}.\vec j.cos(\frac\pi2-\theta)}} = {{r.sin\theta}}\end{cases}\)
Base polaire: \(\vec{OM}=r.\vec{e_r}\)
Base orthonormé: \(\vec{OM}=r.cos\theta.\vec i +r.sin\theta.\vec j\)
Reciproquement:- \(\begin{cases}r={{||\vec{OM}||}}={{\sqrt{x^2+y^2}\\ \theta=arctan(\frac yx)}}\end{cases}\)
\(\longrightarrow\) Vecteurs unitaires - \(\begin{cases}{{\vec{e_r}.\vec i}}={{cos\theta}}\\ {{\vec{e_\theta}.\vec i}}={{-sin\theta}}\end{cases}\)
- \(\begin{cases}{{\vec{e_r}.\vec j}}={{sin\theta }}\\ {{\vec{e_\theta}.\vec j}}={{cos\theta}}\end{cases}\)
Alors:
\(\vec{e_r}=cos\theta.\vec i+sin\theta.\vec j\)
\(\vec{e_\theta}=-sin\theta.\vec i+cos\theta.\vec j\)
\(\triangleright\) Calcul de \(\frac{d\vec{e_r}}{d\theta}\) et \(\frac{d\vec{e_\theta}}{d\theta}\)
- \(\frac{d\vec{e_r}}{d\theta}={{\frac{d}{d\theta}(cos\theta.\vec i+sin\theta.\vec j)}}={{-sin\theta.\vec i + cos\theta .\vec j}}\)
\(\to\) \(\frac{d\vec{e_r}}{d\theta}={{\vec{e_\theta} }}\)
- \(\frac{d\vec{e_\theta}}{d\theta}={{ -\vec{e_r} }}\)
\(\to\)Remarque:
- \(\frac{d\vec{e_\theta} }{d\theta} \perp \vec {e_r}\)
- \(\frac{d\vec{e_r} }{d\theta}\perp \vec {e_r}\)
Vitesse en coordonnées polaires
Accélération coordonnées polaires
Exemples
\(\triangleright\) Mouvement circulaire uniforme
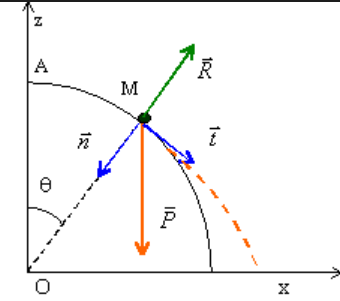
$$\overrightarrow{OM}=R\vec e_r$$
\(\longrightarrow\)Vecteur vitesse angulaire:
$$\vec \omega={{\frac {d\theta}{dt} }}={{\frac {2\pi}{T} }}=\omega \vec k$$
\(T\): période
\(\longrightarrow\)Vecteur vitesse:
$$\vec v={{R.\overset . \theta.\vec e_\theta}}={{R.\omega .\vec e_\theta}}$$
Car \(R\) est constante\(\Rightarrow\) \(\overset . R=0\)
Mouvementt uniforme\(\implies\) \(||\vec v||=constante\) \(\implies\)$\omega=constante\(
\)\longrightarrow\( Vecteur accélération:
\)$\vec a=-R\omega^2\vec e_r$$
L'accélération est centripète
